Введение в конечные автоматы
Конечный автомат (в современной
англоязычной литературе используется также более выразительное, на взгляд
автора, обозначение, не имеющее хорошего русского эквивалента — state
machine, дословно переводимое как машина состояний) представляет
собой устройство, имеющее внутреннюю память (переменные состояния), а
также набор входов и выходов. Объем внутренней памяти у конечных автоматов,
как следует из названия, конечен. Автоматы с неограниченным объемом внутренней
памяти называются бесконечными автоматами,
нереализуемы и используются только в теоретических Построениях (Минский
1971].
Однако некоторые разновидности теоретически бесконечных автоматов — например,
стековые — могут быть реализованы в форме автоматов с практически неограниченной
памятью — например, достаточно глубоким стеком — и находят практическое
применение, например при синтаксическом анализе языков со вложенными структурами
[Кормен/Лейзерсон/Ривест 2000].
Работа автомата состоит в том, что он анализирует состояния своих входов,
и, в зависимости от значений входов и своего внутреннего состояния, изменяет
значения выходов и внутреннее состояние. Правила, в со ответствии с которыми
происходит изменение, описываются таблицей
или диаграммой переходов. Диаграмма переходов
представляет собой граф, вершины которого соответствуют допустимым состояниям
внутренних переменных автомата, а ребра — допустимым переходам между ними.
Переходы между вершинами направленные: наличие перехода из А в В не означает,
что существует переход из В в А. Наличие перехода в обоих направлениях
символизируется двумя ребрами, соединяющими одну пару вершин. Такой граф
называется ориентированным [Кормен/Лейзерсон/Ривест 2000]. Таблица переходов
может рассматриваться как матричное представление диаграммы переходов.
Блок-схемы (рис. 10.5) являются обычным способом визуализации графов переходов
и используются для описания алгоритмов с 60-х годов. Любой алгоритм, исполняющийся
на фон-неймановском компьютере с конечным объемом памяти (а также любой
физически исполнимый алгоритм), может быть описан как конечный автомат
и изображен в виде блок-схемы.
У конечных автоматов с ограниченным числом допустимых значений входов,
граф переходов всегда конечен, хотя и может содержать циклы (замкнутые
пути) и контуры (совокупности различных путей, приводящих к одной и той
же вершине). Понятно, что для автомата с графом, содержащим циклы, невозможно
гарантировать финитности — завершения работы за конечное время. Как известно,
задача доказательства финитности алгоритма, хотя и решена во многих частных
случаях, в общем случае алгоритмически неразрешима [Минский 1971].
Применительно к драйверам внешних устройств, циклический граф может соответствовать
повторным попыткам выполнения операции после ее не-'удачи. Понятно, что
на практике количество таких попыток следует ограничивать. Самый простой
способ такого ограничения — введение счетчика попыток. Формально после
этого состояния с различными значениями счетчика превращаются в наборы
состояний, а граф переходов становится ациклическим (рис. 10.6), но для
достаточно большого количества повторений опять-таки необозримым, поэтому
на практике часто используют сокращенную блок-схему, в которой состояния
с разными значениями счетчика цикла изображаются как одно состояние.
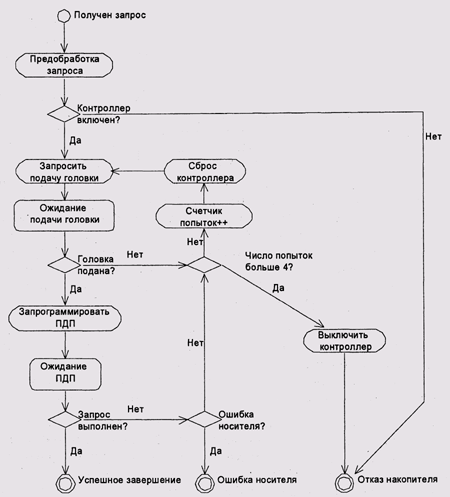
Рис. 10.5. Блок-схема драйвера
Анализ полной или сокращенной блок-схемы алгоритма методами
теории графов, хотя и не может однозначно дать ответ на вопрос о его финитности,
может оказать значительную помощь в оценке алгоритма, в том числе и в
поиске "узких" с точки зрения финитности мест. В [Кнут 2000)
приводятся примеры такого анализа для некоторых простых алгоритмов.
Алгоритмы основной массы реально применяемых программ (особенно использующих
переменные состояния большого объема) имеют совершенно Необозримые блок-схемы.
Отчасти это обходится декомпозицией программного комплекса на отдельные
модули с более обозримой функциональностью и алгоритмом, но все-таки далеко
не для всех алгоритмов представление в виде конечного автомата естественно.
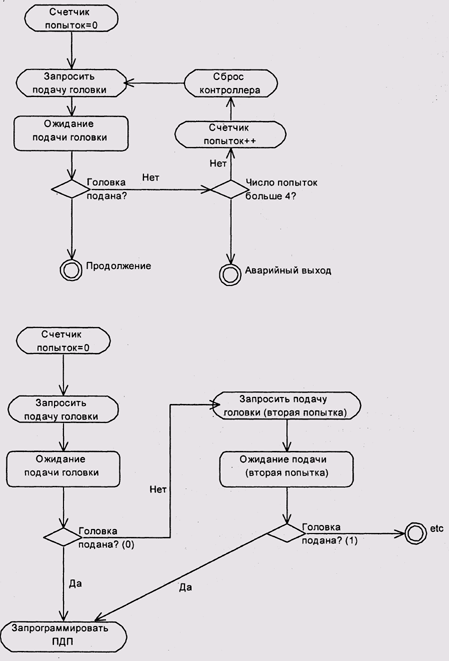
Рис. 10.6. Развертывание циклов в графе состояния
С другой стороны, ряд даже довольно сложных алгоритмов
естественным образом описывается автоматами с небольшим числом состояний,
которые могут быть закодированы одной скалярной переменной состояния или
стеком таких переменных. Такие автоматы находят применение в самых разнообразных
задачах: лексическом и синтаксическом разборе контекстно-свободных и многих
типах контекстно-связанных языков [Кормен/ Пейзерсон/Ривест 2000 1, реализации
сетевых протоколов, задачах корпоративного документооборота (Керн/Линд
2000] и др. В частности, легко понять, что обсуждаемый нами алгоритм драйвера
относится именно к этой категории алгоритмов.
Два основных подхода к реализации конечных автоматов — это
развернутые (unrolled) автоматы и автоматы
общего вида. Примером развернутого конечного автомата является
код основной нити примера 10.2. Понятно, что развертыванию поддаются только
автоматы с весьма специфической — линейной или древовидной — структурой
графа состояний, и если в процессе уточнения требований мы выясним, что
структура автомата должна быт более сложной, нам придется полностью реорганизовать
код.
Автомат общего вида выглядит несколько сложнее, но, научившись распознавать
его конструкцию, легко разрабатывать такие программы по задан ной блок-схеме
и, наоборот, восстанавливать граф состояний по коду программы. Главным
преимуществом грамотно реализованного конечного автомата является легкость
модификации: если граф переходов измените нам надо будет изменить код
только тех узлов, которые затронуты изменением.
Примеры реализации конечных автоматов такого типа на процедурном языке
программирования приводятся во многих учебниках программированию например
[Грогоно 1982). Чаще всего реализация состоит из цикла, условием выхода
из которого является достижение автоматом финального состояния, и размещенного
в теле цикла оператора вычислимого перехода с переменной состояния в качестве
селектора. Конечный автомат, похожий на эту классическую реализацию, приведен
в примере 10.4.
Пример 10.4. Конечный автомат драйвера
контроллера IDE/ATA для OS/2
VOID NEAR StartSM( NPACB npACB )
}
/* ------------------------------------------------ */
* Проверка счетчика использований АСВ*/
/* -------------------- */
/* Автомат реентрантен для каждого АСВ / *
/* ------------------------------------------------ */
DISABLE
npACB->UseCount++;
iff npACB->UseCount == 1 )
{
do
{
ENABLE
do
{
npACB->Flags &= ~ACBF_WAITSTATE;
switch (npACB->State) {
case ACBS__START :
StartState(npACB);
break;
case ACBS_INTERRUPT:
InterruptState(npACB);
break;
case ACBS_DONE:
DoneState(npACB);
break;
case ACBS_SUSPEND:
SuspendState(npACB);
break;
case ACBS_RETRY:
RetryState(npACB);
break;
case ACBS_RESETCHECK:
ResetCheck(npACB);
break/case ACBS_ERROR:
ErrorState(npACB);
break;
while ( !(npACB->Flags & ACBF WAITSTATE) );
DISABLE
I
while ( — npACB->UseCount ) ;
Конечный автомат драйвера OS/2
Несмотря на простоту, пример 10.4 нуждается в комментариях. Параме! функции
startSM — АСВ (Adapter Control Block — блок
управления адаптере! так в OS/2 называется блок переменных состояния устройства).
АСЗ содержит указатель на очередь запросов IORB
(Input/Output Request Block — блок запроса на ввод/вывод) и скалярную
переменную state, которая указывает, в како состоянии сейчас находится
обработка первого запроса в очереди. По коду этого состояния определяется,
какую функцию следует вызвать. В телах этк функций, в зависимости от результата
операции, происходит установка следующего значения переменной состояния
и, возможно, флага ACB_WAITSTATE.
Функция startSM (Start State Machine) вызывается
как из функции обработн запросов, так и из обработчика прерывания. Поэтому
перед входом в собс венно автомат и после выхода из него стоит код, использующий
поле nрАСЕ >UseCount как флаговую переменную,
чтобы не допустить одновременного входа в автомат из обоих возможных нитей
исполнения. Обратите также внимание, что макросами ENABLE
и DISABLE (запрет и разрешение прерываний окружена
работа с флаговой переменной, но не сам автомат.
(В качестве упражнения читателю предлагается понять, как же обеспечиваете
вызов функции interruptstate, если во время прерывания основной поте драйвера
все еще находился в теле автомата.
Полный текст драйвера IDE/ATA для OS/2 включен в стандартную поставку
DDK (Driver Development Kit— набор инструментов [для] разработчика драйверов),
который может быть найден на сайте [www.ibm.com OS/2
DDK].
Построенный нами в примере 10.3 код внешне совсем не
похож на приме 10.4, но, в действительности, также представляет собой
конечный автомат в качестве переменной состояния используется переменная
fdd->handier, в качестве дискретных значений этой переменной
— указатели на функции обрабатывающие конкретные состояния.
|








